先日、出張の折に空港のロビーでこんなものを見つけた。

マッサージチェアが2台並んでいて「無重力マッサージ」と書かれた看板がおいてある。1回の時間は15分、料金は300円とのこと。長旅の前だったのでやっておこうかと思ったがあいにく2台とも使用中であった。二人がいつ始めたのかはわからない。最大15分待てば絶対に空くのはわかるのだが。二人が始めた時間がランダムだとして私は平均どれだけ待てばいい計算になるだろうか。
もしもマシンが1台だけならば、待ち時間は0分から15分までばらつくはずなので平均待ち時間は15分の半分の7.5分になるのはわかる。それが2台になるとどうなるかという問題である。
考えているうちに5分ほど経過したところで片方のマシンが終了して止まった。すかさず乗り込んで硬貨を投入するとマシンは音もたてずに動き出した。両足、両腕が包み込むように固定される。すぐに背中から心地よい振動が伝わってきた。やがてマシン全体の姿勢があおむけになるように傾いて無重力状態となった。15分という時間はマッサージとして短すぎると思ったのだが、肩、背中は勿論、足、足裏、腕を同時にマッサージするのでなかなか効率がいい。私は夢見心地になりながらさきほどの続きを考え始めた。
待ち時間については一般の場合を考慮して次の関数を定義する。

待ち時間については下図のような絵で考える。
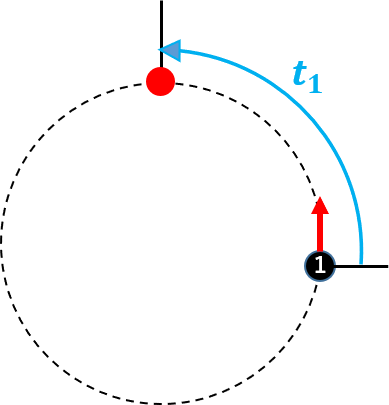
本図で上部が私が待ち始めた時間を示し、マシンはこの円上を私に向かって進んできて到着した時点がマシンが終了したことを表す。一周はマシン1回分の時間を示している。今回の場合だと15分ということになるが計算を簡略化するためにこれを単位時間:1とする。15分の場合ならば結果を15倍すればいい。
このようにまずマシンが1台の場合の待ち時間の平均値は、さきほどの表記方法を用いて、
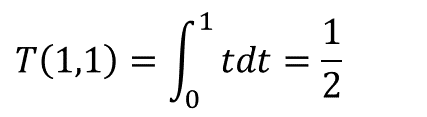
となる。つまり半分の7.5分である。次にマシンが2台の今回の場合である。
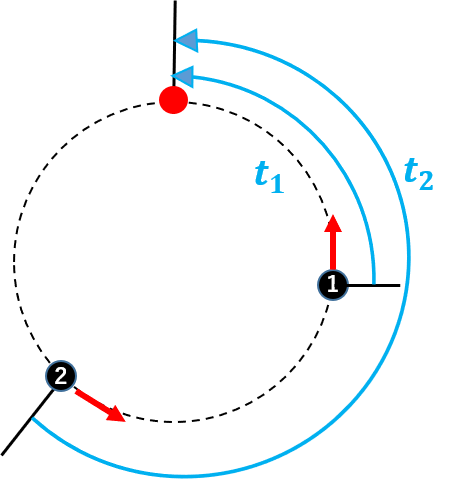
マシンに1,2という番号を付けているが本図ではマシン1が先に終わる場合を示しているが当然、逆の場合もありうる。この場合の待ち時間を計算すると、
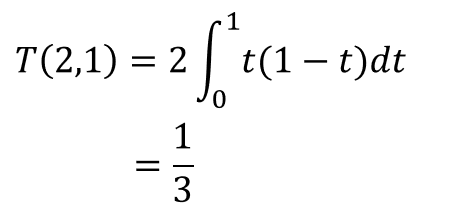
となる。2倍しているのが2台の中でどちらが早いかの通りに対応している。結果は3分の1、つまり5分となる。さてここではマシン2台だったが、一般にn台の場合についても計算してみると、
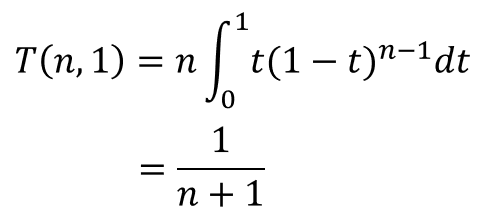
が得られる。nが増えるに従って待ち時間は0に近づいていく。分母はマシンの台数+1である。この+1は邪魔でわかりにくい。この正体はなんなのだろう。
さてそうこう考えているうちにもう一方のマシンも終了した。気づかないうちに次に使いたい人たちが並んで待っていた。若い男女の二人連れだった。しかし一方が空いたのに乗ろうとしない。男性の方はマー君と呼ばれていたが、どうやらこの2人は2台で同時に始めたいので両方が空くまで待っているようだった。やがて私の方も15分が経過して終了し、二人は念願かなって2台のマシンに乗り込み仲良く並んで同時に動き出した。
マー君たちのやり方だと2台終わるまで待つ必要があるがこの時、平均待ち時間はどうなるだろう。私の場合は5分だったが当然それよりも長いことは確かだろう。それを計算してみると、
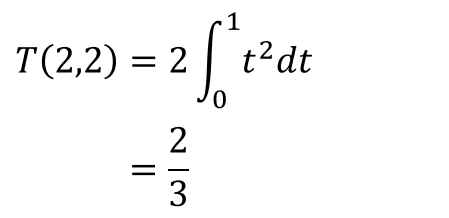
結果は3分の2、つまり10分と私の2倍必要なことが分かった。マー君のやり方をさらに拡張して、n台のマシンでn人のグループが全台が終了するまで待つときの平均待ち時間は、
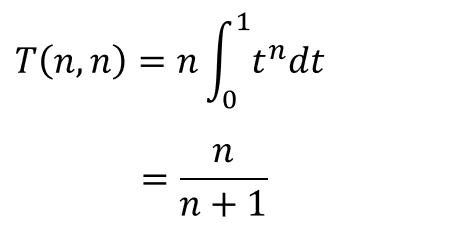
となる。マシンが増えるに従って単位時間1、つまり15分にどんどん近づいていく。
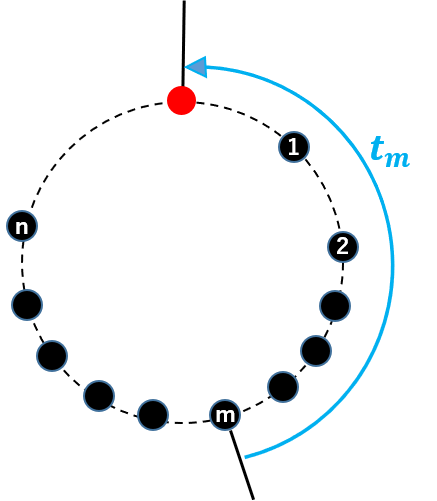
さらに一般の場合を考える。稼働中のマシンがn台で、その中でm台が終了するまで待つ場合である。
この場合の平均待ち時間の計算式は、
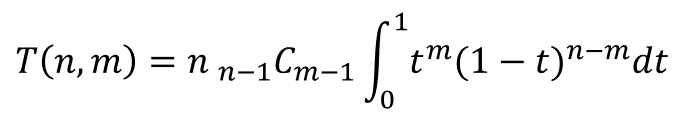
となる。積分の前の項の意味は、

である。まず、積分項である、
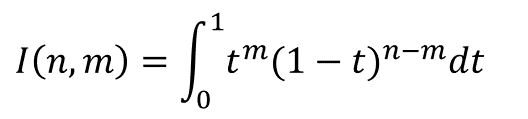
の計算が必要となる。部分積分をひたすら繰り返してもいいのだが、ここでは被積分関数が2項定理に似た形をしていることに着目して、次の2項展開を利用する。ここで係数αを導入している。
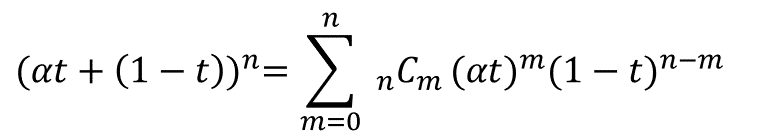
左辺を積分すると、
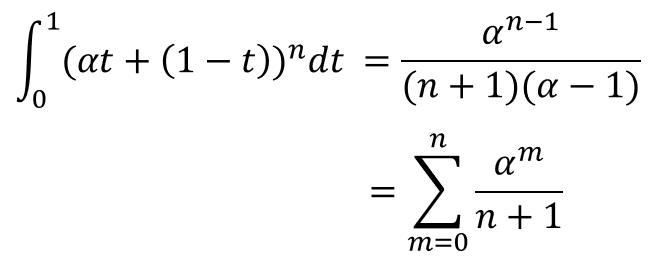
と、αのn次多項式となる。同様に右辺は、
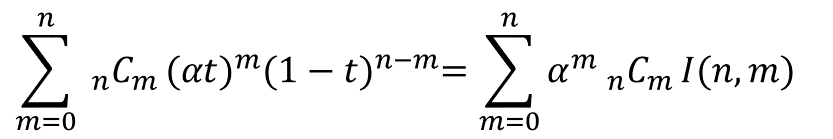
となる。αの係数を比較することで、
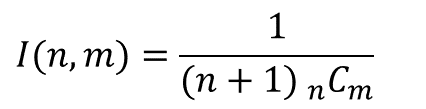
が得られ、これを用いて平均待ち時間は、
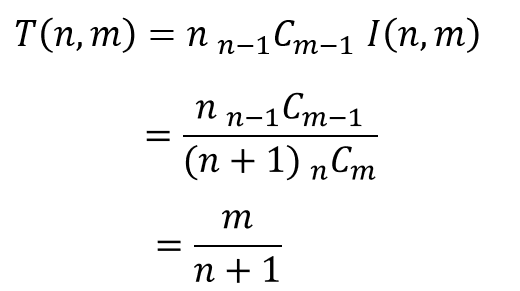
という大変シンプルな式で表されることが分かった。
この式は直感的にどう理解すればいいだろうか。
そもそも本問題で登場するタイミングを考えてみると、マシンn台のn個は勿論であるが、それに加えて今回の私やマー君のように利用客のタイミングが存在し、待ち時間はこれらn+1のランダムなタイミングの相互関係で決定される。
平均値についてはこれらn+1のタイミングが最も均等に分散した場合の待ち時間時間であると考えられる。つまりn+1個が下図のこのように等間隔に並んだ場合と等しいと考えることができるのである。
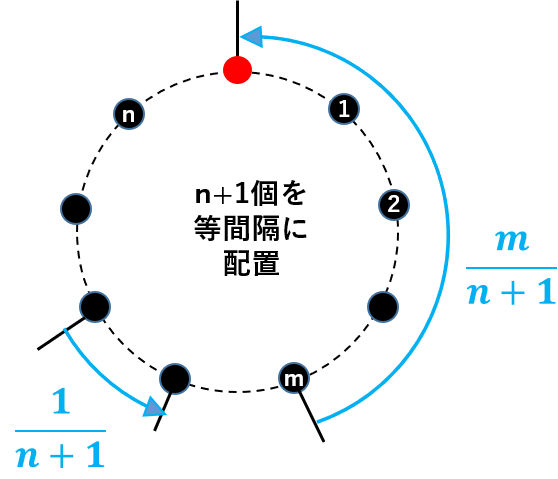
つまり分母に登場して邪魔だとばかり思っていた「+1」の正体は他ならぬ私自身であった。