
2次元平面である点を原点を中心に角度θだけ回転させる。

この時の座標の変換は次の行列Rで記述されることはよく知られている。

これを3次元に拡張する。
3次元の場合は回転する方向が自由に選べるので回転軸を定義する必要がある。いきなり3次元の話を始める前に、2次元の回転の場合でもz軸を想定してそれを軸とした回転を考えるところから始めるのがわかりやすい。
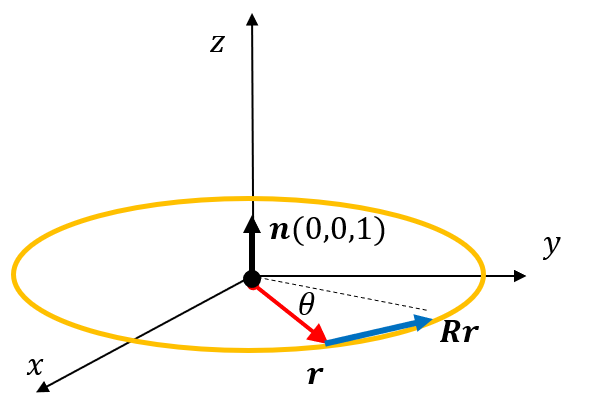
z軸方向の単位ベクトルをnとする。この時、回転の方程式は、

となる。回転で原点からの距離が不変であること、つまり回転の軌跡が円であることは、

であることからわかる。ここで位置ベクトルrと回転のベクトルnxrが垂直であることを用いた。
上記の方程式を座標を用いて表すと、

となる。ここで登場するx、yについてはともに、

という微分方程式を満足する。これの一般解は、

であり、適当な初期条件で解くことにより、上記の回転行列Rが求められる。
さて、3次元の場合の回転行列を考える。

ここでnは回転軸方向の単位ベクトルであり、

を満たす。
この時の回転の微分方程式は、

となる。2次元の場合とは異なり複雑であり、簡単に計算できそうには見えない。この解法として線形代数における対角化を用いることにする。まずはその練習として、2次元の場合に適用してその効果を検証してみる。
先に示した回転の微分方程式は、

となり、ここに行列Aが定義される。

行列Aを対角化するために固有値を求めると、iを虚数単位として、

となる。これらに対応した固有ベクトルは、

となるので、行列Aは、

という行列Pを用いて対角化可能である。

このように対角成分には固有値が並ぶ。対角化後の微分方程式は容易に解けて、次の行列Bで表現される。

これを用いることで2次元の場合の回転行列は、

が求められる。
さて、この解法を3次元の場合に適用する。先に述べた微分方程式は、行列を用いて表現すると、

となる。この行列Aについて対角化を行う。


固有値の中に0があるのは、この行列Aが正則でないことに対応している。行列Aは次の行列Pで対角化可能である。

行列Pの逆行列は、

であり、行列AはPにより、

と対角化される。対角化後の微分方程式は容易に解けて次の行列Bが得られる。

これを用いて3次元の回転行列Rは、

となる。一見して決して美しいとは言えない。しかしこのRには次の特徴がある。

つまりユニタリ行列である。また、

回転軸の方向ベクトルnはRの固有ベクトルである(固有値λは1)。実際に計算してみると、次の式が見事に成り立つ。

これらの特徴を使って次のことが証明される。

これは行列Rで変換されるrは必ずベクトルnに垂直な平面上にある、ということを示している。そしてその平面の方程式は、

である。