前回に引き続き、スーパーボールの挙動についてである。
今回は連続して衝突が発生する場合を考える。そのために準備をする。
スーパーボールの床面との衝突運動は、前回の説明のとおり、運動量の保存則、そしてエネルギーの保存則である次の2式に従う。
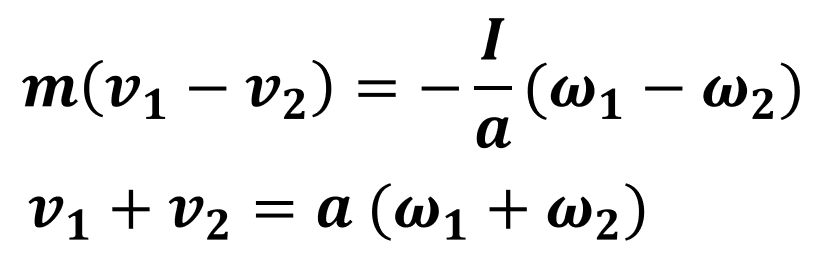
これをv、 ωの連立方程式として解くと、
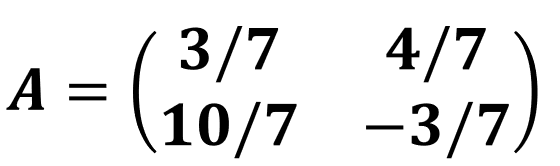
なる行列Aを用いて、
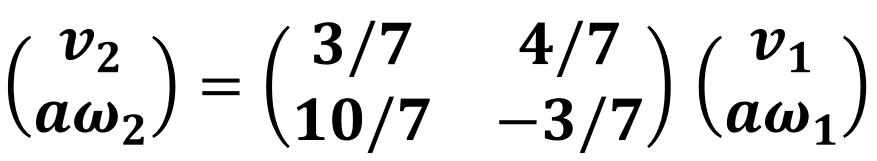
という形で表すことができる。これを用いると行列計算によって運動を計算することが可能となる。
実はこの行列Aについては、
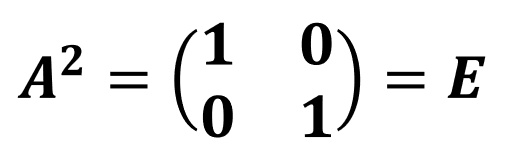
という特徴がある。ここで行列Eは単位行列である。これが意味するところは、2回床面に衝突すると再びもとの運動に戻る、ということになる。この特徴については具体的なケースで説明する。
◆連続衝突:水平速度なしの場合
ボールをまっすぐ下に落とす場合である。その際、ボールに回転を加えなければ、

同じ位置にとどまって、上下運動を繰り返すだけである。これに対してボールを離す時に回転を加えてみると、
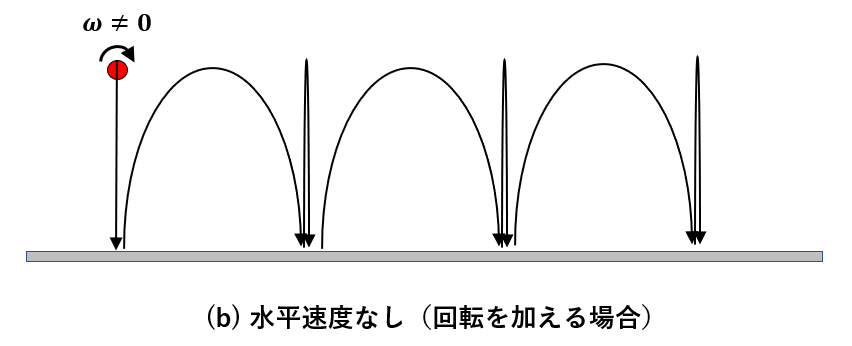
回転方向に移動を開始する。反対に回せば逆の方向に進む。その際、移動する運動と単なる上下運動を交互に繰り返す。これがさきほど述べた、行列Aの2乗が単位行列になることに対応している。
◆連続衝突:水平速度ありの場合
続いて、ボールの水平方向の速度をつけて放り投げる場合を考える。放り投げる際に与える回転数に応じて挙動が異なる。ωの大きさに対応した挙動を下図に示す。
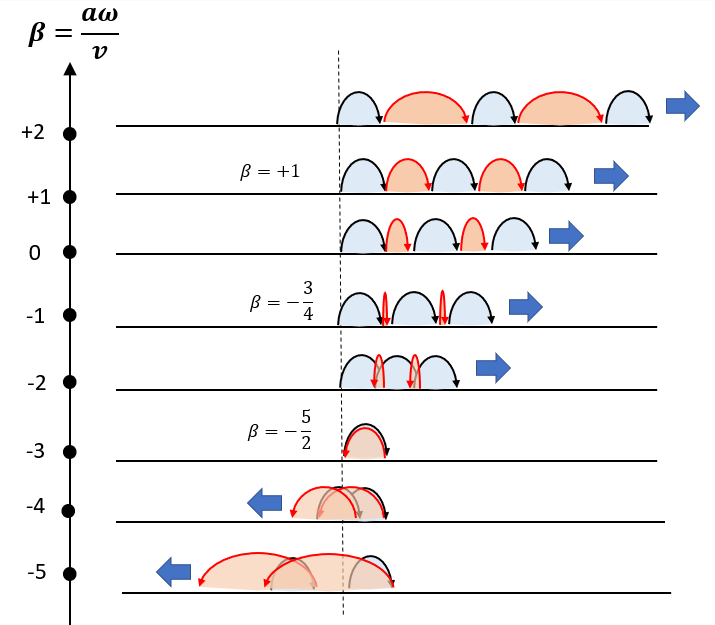
この場合においても2種類の動作を交互に繰り返すことは同様である。2種類を青色、赤色で識別している。
(1) β=-5/2の場合が前回説明した振動する条件である。それ以上ならば全体として右方向、それ以下ならば左方向に移動していく。
(2) β=+1の場合が前回説明したスーパーボールらしからぬ挙動である。
(3) β=-3/4の場合は、2度目の動きは単純に上下する運動である。上述の(b)の挙動と同じである。
さて、以上のケースはすべて2通りの形が交互に現れるというルールはきちんと守られているがそれが守られないケースは存在しないのであろうか。実はそれは身近に存在する。それは挟まれた2枚の板の間の空間でボールが両方に衝突する場合である。
◆連続衝突:上下2枚の板に仕切られた空間内での運動
2枚に仕切られていたとしても、個々の衝突は同じ法則に基づくと考えてしまいがちであるが、実はボールの回転方向に対する摩擦力の方向が2枚の板でちょうど逆の関係になる。仮に下側の板での衝突運動を表す行列を、
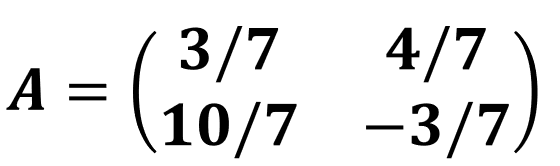
という前述と同じであるとすると、もう一方の上側の板との衝突については、行列の一部の符号が反転して、

となる。この場合は、行列A、行列Bが交互に作用することになり、運動は一転して複雑化する。その一例としてボールを回転させずに投げた場合のボールの軌跡がどうなるかを計算で10回目の衝突まで求めた結果を下図に示す。
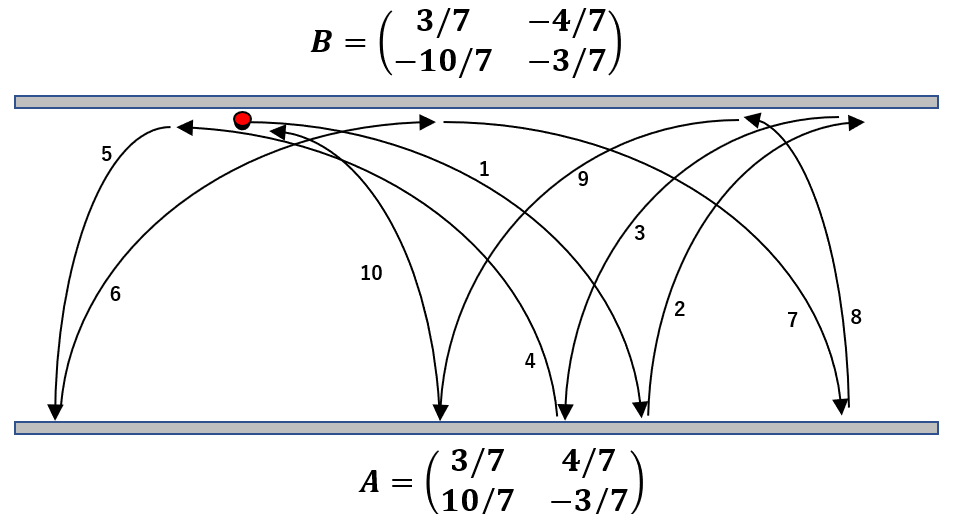
実際にスーパーボールでこれを試してみると、運動は複雑で何が起きているのかわかりにくいものの、ある決められた範囲の中でうろうろと迷走している雰囲気だけは観測できる。
特に最初の1→2→3→4でボールは手元に戻ってくる。これなどは会社のデスクなどを使ってすぐに実験できるのでチャレンジされたい。